Monthly Archives: August 2010

Astronomy

My web-based observatory images (Pluto, Jupiter, Saturn, Uranus, Orion Nebula)

Leave a comment

There are some web-based observatories which allow normal people like you and I to rent a telescope somewhere on this planet for a short period of time and quite reasonable amount of money, to take some pictures. Not only is the available equipment superior to the scopes that many people have at home (at least to me this applies for sure), these scopes are most often located on very favorable places up on a mountain, far from city lights and likely good weather conditions. One of these web-based observatories is Global-Rent-a-Scope or short GRaS, where I made my first steps.

They have telescopes in Australia (which adds another advantage: you can take pictures of the Southern Sky, even if you live in fairly high Northern Latitudes; this is also true the other way around of course), Spain (this one is relatively new) and the one which I’ve been using for my tests so far, Mayhill, New Mexico at 32° 54′ 3.60″ N, 105° 31′ 26.41″ W.

My latest achievement was to take 2 images of dwarf planet Pluto, the first on August 23, 2010 at 05:25 UTC and the second on August 27, 2010 at 03:11 UTC. I cut the images to show the same area of the sky, so you can open the images in new browser tabs, switch back and forth between them, and I think you should be able to spot the “pixel” which is Pluto that has changed its location significantly, while the surrounding stars stay at the same positions:

pluto-gras-20100823052500  pluto-gras-20100827031100

If you didn’t manage to spot Pluto, here is the same sky area with Stellarium (an awesome piece of astronomical software … Open Source and available for all the major platforms):

pluto-stellarium-20100823052500  pluto-stellarium-20100827031100

You can also view the original Pluto image of August 23 and the original Pluto image of August 27. The unedited Stellarium screenshots are also available, for August 23 and August 27.

This is something which I could never do with the binoculars and the telescope which I have at home. Pluto, with a magnitude of around 14, is beyond my capabilities (whether it's limited by my technical capabilities or just my skills is yet to be found out).

Here are some more images which I have taken through scopes provided by GRaS (all in Mayhill, NM).

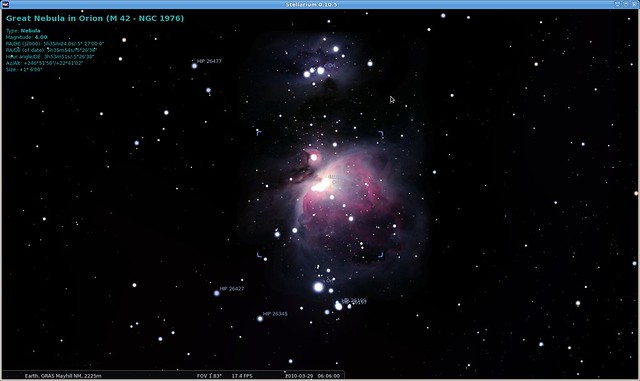
Orion nebula on March 29, 2010 at 4:06 UTC

orion_nebula-gras-201003290406  orion_nebula-stellarium-201003290406

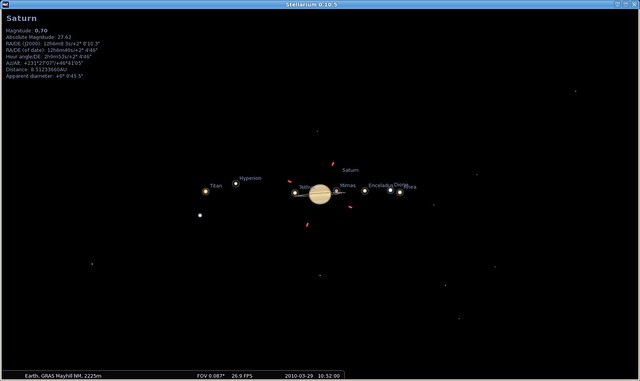
Saturn on March 29, 2010 at 8:52 UTC with Saturnian moons Titan, Enceladus, Dione and Rhea visible

saturn-gras-1-201003290852  
saturn-gras-2-201003290852  saturn-stellarium-201003290852

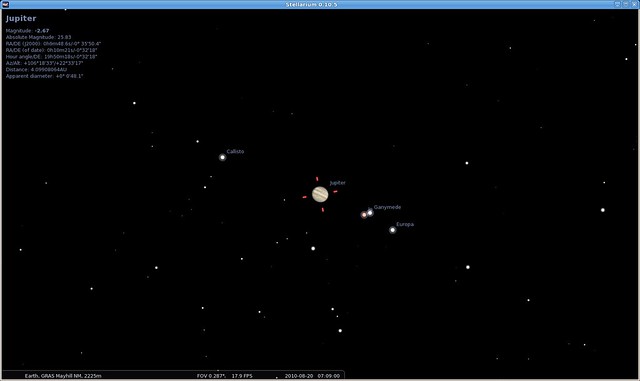
Jupiter on August 20, 2010 at 5:09 UTC with Jovian moons Callisto, Io, Ganymede and Europa visible

jupiter-gras-201008200509  jupiter-stellarium-201008200509

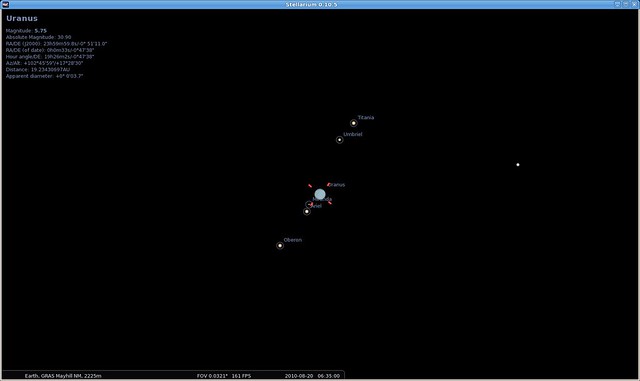
Uranus on August 20, 2010 at 6:35 UTC with Uranian moons Titania, Umbriel and Oberon visible

uranus-gras-201008200635  uranus-stellarium-201008200635

PlanetMySQL, WWW

How to do user language/locale detection quickly without Zend Framework

Leave a comment

Recently I wrote about detecting the preferred language or locale of a web site visitor, using Zend Framework.

Well, I have to start with one correction. In my last blog post about this topic I talked about the User Agent String, but since I wrote the article, I figured out that the User Agent String doesn’t play any role at all. Neither in the Zend Framework variant that I blogged about earlier, nor in today’s code. And that is good so, because both Internet Explorer and Mozilla Firefox will no longer add the browser language or locale to their User Agent Strings in the future. Other browsers are likely to follow, since there are efforts to make it harder to fingerprint users by their UA-Strings.

So here is my ZF-less variant:

$m = array();
$http_accept_language = 
   isset($_SERVER['HTTP_ACCEPT_LANGUAGE']) ? 
     $_SERVER['HTTP_ACCEPT_LANGUAGE'] : 
     "";
preg_match_all('/([a-z]{2})(?:-[a-zA-Z]{2})?/', 
               $http_accept_language, 
               $m);

$pref_locale = array();
foreach($m[0] as $locale) {
    $pref_locale[] = $locale;
}

$pref_lang = array();
foreach($m[1] as $lang) {
    if (! in_array($lang, $pref_lang)) {
        $pref_lang[] = $lang;
    }
}

The array $pref_locale will contain all locales in order of the user’s preference, and $pref_lang will only contain the languages in order of the user’s preference. Other than my ZF code from last time, this allows to look up secondary, tertiary etc. choices of the user as well.

Here is an example. Lets assume, these are the user’s preference settings:

$_SERVER['HTTP_ACCEPT_LANGUAGE'] would contain:

en-us,en;q=0.9,de-at;q=0.7,de;q=0.6,es-es;q=0.4,es;q=0.3,ja;q=0.1.

After running my code, the $pref_locale array would contain this:

Array
(
    [0] => en-us
    [1] => en
    [2] => de-at
    [3] => de
    [4] => es-es
    [5] => es
    [6] => ja
)

and the $pref_lang array would contain

Array
(
    [0] => en
    [1] => de
    [2] => es
    [3] => ja
)

Still simple enough, and most importantly, still a better solution than what Google still does.

Browser, Firefox, WWW

Running multiple Firefox versions & profiles at the same time

Leave a comment

Oh my freaking Flying Spaghetti Monster!

I used to think that I know Mozilla applications like Firefox and Thunderbird quite well.

Now I’m wondering, how could I miss this feature that I’ve been wishing for so long? And actually, it was very near the top of my most wanted features that I wished Mozilla would implement. Today I found out, it’s been there for many years.

It is, as the subject says, to run multiple versions of Firefox, or Thunderbird, at the same time. Especially at times like these, as Firefox 4.0 is baking and becoming increasingly suitable as a day-to-day browser, while still having a few flaws which sometimes want me to refer back to version 3.6, this may be extremely useful.

However, even if you have 2 versions of Firefox installed. As long as one version is running, and you try to start an instance of the other version by just starting Firefox the “normal way”, you get a new window of the version which is already running. But there is a solution.

And it’s very simple. It’s important to have different profiles as well (this is something that I would recommend anyway, never run different versions on the same profile – it can get pretty messed up). They are easy to create, just start Firefox (or Thunderbird) with

firefox -P


I always leave one “naked” profile which I used to call “virgin” 😉

So you need at least 2 profiles. Lets assume we have a profile “ff36” to run Firefox 3.6 on and one profile “ff40” to run Firefox 4.0 on. How to start them? Here is what it could look like (assuming we have Firefox 3.6 in /opt/firefox-3.6 and Firefox 4.0 in /opt/firefox-4.0b4):

/opt/firefox-3.6/firefox -P ff36

This is basically the standard way of starting Firefox with a specific profile. Now lets start the Firefox 4.0 instance:

/opt/firefox-4.0b4/firefox -P ff40 -no-remote

Notice the -no-remote? This is the little piece that does that trick. Without -no-remote you would have gotten just a new Firefox 3.6 window. With it, you get a nice Firefox 4.0 side by side your Firefox 3.6. And here’s what it looks like:

The same works for Thunderbird as well, and probably for most or even all XUL-based applications (SeaMonkey, Songbird, Instantbird are a few that spontaneously come to my mind).

The shocking thing to me was that it has already been introduced in Firefox 2, as the MozillaZine Knowledge Base article told me.